Les règles du sudoku▲
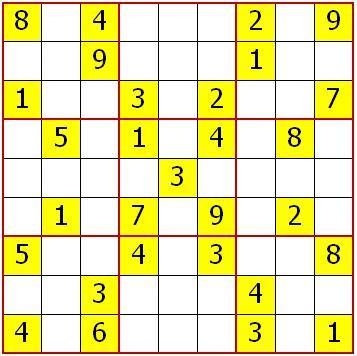
Un plateau de sudoku est composé d'une grille de neuf cases de côté. Ce plateau est divisé en « carrés » de trois cases de côté. Certaines des cases du plateau sont vides, d'autres ont déjà des valeurs associées.
Le but du jeu de sudoku est simple: il faut compléter la grille en respectant les règles suivantes :
- chaque case du plateau peut prendre une valeur allant de 1 à 9 ;
- les cases de chaque ligne ont toutes une valeur différente ;
- les cases de chaque colonne ont toutes une valeur différente ;
- les cases de chaque carré ont toutes une valeur différente.
Pour résoudre ce problème, nous allons écrire un programme Prolog faisant intervenir de la Programmation Logique avec Contraintes.
Programmation Logique avec Contraintes▲
Le terme « Programmation Logique avec Contraintes » (PLC) se traduit en Anglais par Constraint Logic Programming, abrégé CLP. C'est l'une des fonctionnalités qu'offre le langage Prolog (abréviation de PROgrammation LOGique).
Le but de ce didacticiel est d'écrire un programme en Prolog afin de résoudre un sudoku en utilisant la Programmation Logique avec Contraintes.
Le langage Prolog▲
Si vous n'avez jamais programmé en Prolog, vous pouvez découvrir ce langage grâce à mon didacticiel portant sur le sujet :
Le langage Prolog
Vous pouvez également consulter cette page :
http://fr.wikipedia.org/wiki/Prolog
swi-prolog▲
Pour écrire notre programme, nous allons utiliser swi-prolog. Pourquoi? Parce que contrairement à Sictus Prolog (qui propose également des solveurs de contraintes), swi-prolog a l'immense mérite d'être gratuit (c'est vrai que ça aide !).
Cet article illustrera donc la Programmation Logique avec Contraintes en swi-prolog, mais nous exposerons également les quelques différences avec Sicstus Prolog.
Bibliothèque utilisée▲
Il existe plusieurs bibliothèques différentes suivant le type de problème à résoudre ainsi que suivant l'implémentation.
Avec swi-prolog :
- solveur sur domaine fini ('clp/bounds') ;
- solveur sur les réels ('clpr') ;
- consistance d'arc ('clp/clp_distinct').
Avec Sicstus Prolog :
- solveur sur domaine fini (clpfd) ;
- solveur sur les entiers (clpq) ;
- solveur sur les réels (clpr).
Pour écrire notre programme, nous allons utiliser le solveur sur domaine fini de swi-prolog (clp/bounds). Pour utiliser cette bibliothèque, on ajoute la ligne suivante en début de fichier :
:- use_module(library('clp/bounds')).Si on avait voulu utiliser la bibliothèque correspondante dans Sicstus Prolog, on aurait fait cette inclusion à la place :
:- use_module(library(clpfd)).Résolution du problème▲
Étapes de résolution▲
La résolution d'un problème en PLC repose toujours sur les mêmes étapes :
- déclaration des variables ;
- définition des domaines ;
- spécification des contraintes ;
- recherche de solutions.
Nous allons détailler chacune de ces étapes dans les sections suivantes.
Déclaration des variables▲
La Programmation Logique avec Contraintes (PLC) consiste en la représentation de problèmes sous forme d'un ensemble de variables soumises à des contraintes.
La première étape consiste à déclarer ces variables.
Le plateau de jeu est constitué de 81 cases pouvant prendre des valeurs comprises entre 1 et 9. Nous représenterons donc le plateau à l'aide de 81 variables, dont le nom sera constitué de :
- une lettre pour la ligne (A-I) ;
- un chiffre pour la colonne (1-9).
Pour des raisons de commodité (faciliter la définition du domaine de variables), ces variables seront stockées dans une liste :
Vars =
[
A1,A2,A3,A4,A5,A6,A7,A8,A9,
B1,B2,B3,B4,B5,B6,B7,B8,B9,
C1,C2,C3,C4,C5,C6,C7,C8,C9,
D1,D2,D3,D4,D5,D6,D7,D8,D9,
E1,E2,E3,E4,E5,E6,E7,E8,E9,
F1,F2,F3,F4,F5,F6,F7,F8,F9,
G1,G2,G3,G4,G5,G6,G7,G8,G9,
H1,H2,H3,H4,H5,H6,H7,H8,H9,
I1,I2,I3,I4,I5,I6,I7,I8,I9
],Définition des domaines▲
Une fois les variables déclarées, il est nécessaire de définir leur domaine.
D'après les règles du sudoku, chaque case a une valeur comprise entre 1 et 9.
En swi-prolog, on définit les domaines des variables de la manière suivante :
Vars in 1..9,En Sicstus Prolog, on peut définir les domaines de deux manières :
Vars in 1..9,ou :
domain(Vars, 1, 9),Spécification des contraintes▲
La spécification des contraintes a un double but :
- spécifier les contraintes à respecter lors de la recherche de solutions ;
- réduire les domaines des variables avant résolution (consistance d'arc).
Si, lors de la propagation des contraintes et de la réduction des domaines, l'une des variables venait à avoir un domaine vide, le prédicat échouerait et l'exécution s'arrêterait, car aucune solution ne pourrait être trouvée. Ceci se fait de manière automatique.
On spécifie des contraintes grâce aux opérateurs #=, #\=, #<, #=<… (les mêmes opérateurs qu'en Prolog, mais avec un # devant).
On spécifie également des contraintes grâce à des prédicats tels que all_different/1. C'est d'ailleurs ce dernier qui va nous permettre de traduire des règles du sudoku telles que « les éléments d'une ligne sont tous différents » :
% Tous les chiffres d'une ligne sont differents
all_different([A1,A2,A3,A4,A5,A6,A7,A8,A9]),
all_different([B1,B2,B3,B4,B5,B6,B7,B8,B9]),
all_different([C1,C2,C3,C4,C5,C6,C7,C8,C9]),
all_different([D1,D2,D3,D4,D5,D6,D7,D8,D9]),
all_different([E1,E2,E3,E4,E5,E6,E7,E8,E9]),
all_different([F1,F2,F3,F4,F5,F6,F7,F8,F9]),
all_different([G1,G2,G3,G4,G5,G6,G7,G8,G9]),
all_different([H1,H2,H3,H4,H5,H6,H7,H8,H9]),
all_different([I1,I2,I3,I4,I5,I6,I7,I8,I9]),
% Tous les chiffres d'une colonne sont differents
all_different([A1,B1,C1,D1,E1,F1,G1,H1,I1]),
all_different([A2,B2,C2,D2,E2,F2,G2,H2,I2]),
all_different([A3,B3,C3,D3,E3,F3,G3,H3,I3]),
all_different([A4,B4,C4,D4,E4,F4,G4,H4,I4]),
all_different([A5,B5,C5,D5,E5,F5,G5,H5,I5]),
all_different([A6,B6,C6,D6,E6,F6,G6,H6,I6]),
all_different([A7,B7,C7,D7,E7,F7,G7,H7,I7]),
all_different([A8,B8,C8,D8,E8,F8,G8,H8,I8]),
all_different([A9,B9,C9,D9,E9,F9,G9,H9,I9]),
% Tous les chiffres d'un carre sont differents
all_different([A1,A2,A3,B1,B2,B3,C1,C2,C3]),
all_different([A4,A5,A6,B4,B5,B6,C4,C5,C6]),
all_different([A7,A8,A9,B7,B8,B9,C7,C8,C9]),
all_different([D1,D2,D3,E1,E2,E3,F1,F2,F3]),
all_different([D4,D5,D6,E4,E5,E6,F4,F5,F6]),
all_different([D7,D8,D9,E7,E8,E9,F7,F8,F9]),
all_different([G1,G2,G3,H1,H2,H3,I1,I2,I3]),
all_different([G4,G5,G6,H4,H5,H6,I4,I5,I6]),
all_different([G7,G8,G9,H7,H8,H9,I7,I8,I9]),Ensuite, il faudra initialiser le sudoku avec les valeurs initiales du plateau. Pour cela, on écrit un prédicat grid/2 avec comme arguments la valeur du plateau (sous forme d'une liste) et la liste des variables de notre système.
Si la valeur d'une case est à découvrir, on met 0 comme valeur sur le plateau. Si la valeur dans la liste est différente de 0, alors on ajoute la contrainte Variable #= Valeur
Ceci nous donne le prédicat suivant :
grid([],[]) :- !.
grid([0|Q1],[_|Q2]) :-
!,
grid(Q1,Q2).
grid([Val|Q1],[Var|Q2]) :-
!,
Var #= Val,
grid(Q1,Q2).Maintenant, nous avons tout ce qu'il nous faut pour effectuer la recherche de solutions.
Recherche de solutions▲
L'étape précédente a permis la réduction des domaines des variables (quand cela est possible), ce qui facilite la recherche de solutions.
La recherche de solutions consiste à faire la chose suivante :
- choisir l'une des variables ;
- assigner à cette variable une valeur de son domaine ;
- réduire les domaines des autres variables par propagation de contraintes ;
- recommencer avec une autre variable ou revenir en arrière si aucune solution n'existe ;
- lorsque toutes les variables ont été affectées, retourner la solution.
Le choix des variables peut influencer sur le temps de recherche d'une solution. Ce choix se fait en se basant sur certaines heuristiques, comme par exemple choisir en premier la variable ayant le plus petit domaine (c'est pour cela que la réduction de domaine par consistance d'arc est une étape importante). D'autres heuristiques existent, comme par exemple choisir en premier la variable la plus fortement contrainte. Ces heuristiques peuvent être combinées entre elles.
Ce processus se fait de manière automatique par l'usage du prédicat label/1 :
label(Vars),Avec Sictus Prolog, le prédicat est différent: il s'agit de labeling/2 et a deux arguments, le premier étant une liste d'options pour la recherche de solutions (la liste vide [] correspondant aux options par défaut) :
labeling([ffc,step,up,all], Vars),Programme et exécution▲
Programme▲
Maintenant que nous avons détaillé chacune des étapes de la représentation du problème en PLC, nous pouvons avoir une vue d'ensemble du programme.
Dans notre programme final, nous avons ajouté quelques prédicats pour l'affichage du plateau de jeu dans un format lisible :
:- use_module(library('clp/bounds')).
/*
Permet de résoudre un sudoku
Entrée: +Grid: la grille de sudoku (0 => vide, [1-9] => ajoute une contrainte)
Sortie: -Vars: une solution (permet de savoir s’il existe plusieurs solutions)
*/
sudoku(Grid, Vars) :-
% Definition des variables (grille de sudoku)
Vars =
[
A1,A2,A3,A4,A5,A6,A7,A8,A9,
B1,B2,B3,B4,B5,B6,B7,B8,B9,
C1,C2,C3,C4,C5,C6,C7,C8,C9,
D1,D2,D3,D4,D5,D6,D7,D8,D9,
E1,E2,E3,E4,E5,E6,E7,E8,E9,
F1,F2,F3,F4,F5,F6,F7,F8,F9,
G1,G2,G3,G4,G5,G6,G7,G8,G9,
H1,H2,H3,H4,H5,H6,H7,H8,H9,
I1,I2,I3,I4,I5,I6,I7,I8,I9
],
%%%%% REGLES DU JEU %%%%%
% Les cases prennent des valeurs de 1 a 9
Vars in 1..9 ,
% Toutes les valeurs d'une ligne sont differents
all_different([A1,A2,A3,A4,A5,A6,A7,A8,A9]),
all_different([B1,B2,B3,B4,B5,B6,B7,B8,B9]),
all_different([C1,C2,C3,C4,C5,C6,C7,C8,C9]),
all_different([D1,D2,D3,D4,D5,D6,D7,D8,D9]),
all_different([E1,E2,E3,E4,E5,E6,E7,E8,E9]),
all_different([F1,F2,F3,F4,F5,F6,F7,F8,F9]),
all_different([G1,G2,G3,G4,G5,G6,G7,G8,G9]),
all_different([H1,H2,H3,H4,H5,H6,H7,H8,H9]),
all_different([I1,I2,I3,I4,I5,I6,I7,I8,I9]),
% Toutes les valeurs d'une colonne sont differentes
all_different([A1,B1,C1,D1,E1,F1,G1,H1,I1]),
all_different([A2,B2,C2,D2,E2,F2,G2,H2,I2]),
all_different([A3,B3,C3,D3,E3,F3,G3,H3,I3]),
all_different([A4,B4,C4,D4,E4,F4,G4,H4,I4]),
all_different([A5,B5,C5,D5,E5,F5,G5,H5,I5]),
all_different([A6,B6,C6,D6,E6,F6,G6,H6,I6]),
all_different([A7,B7,C7,D7,E7,F7,G7,H7,I7]),
all_different([A8,B8,C8,D8,E8,F8,G8,H8,I8]),
all_different([A9,B9,C9,D9,E9,F9,G9,H9,I9]),
% Toutes les valeurs d'un carre sont differentes
all_different([A1,A2,A3,B1,B2,B3,C1,C2,C3]),
all_different([A4,A5,A6,B4,B5,B6,C4,C5,C6]),
all_different([A7,A8,A9,B7,B8,B9,C7,C8,C9]),
all_different([D1,D2,D3,E1,E2,E3,F1,F2,F3]),
all_different([D4,D5,D6,E4,E5,E6,F4,F5,F6]),
all_different([D7,D8,D9,E7,E8,E9,F7,F8,F9]),
all_different([G1,G2,G3,H1,H2,H3,I1,I2,I3]),
all_different([G4,G5,G6,H4,H5,H6,I4,I5,I6]),
all_different([G7,G8,G9,H7,H8,H9,I7,I8,I9]),
%%%%% VALEUR DU PLATEAU %%%%%
grid(Grid, Vars),
%%%%% RECHERCHE DE SOLUTIONS %%%%%
label(Vars),
% Affichage
printGrid(Vars).
/*
Permet d'initaliser la grille de sudoku
Pour chaque élément différent de 0,
ajoute la contrainte Var #= Val
*/
grid([],[]) :- !.
grid([0|Q1],[_|Q2]) :-
!,
grid(Q1,Q2).
grid([Val|Q1],[Var|Q2]) :-
!,
Var #= Val,
grid(Q1,Q2).sudokuExemple(Vars) :-
sudoku(
[ 8,0,4,0,0,0,2,0,9,
0,0,9,0,0,0,1,0,0,
1,0,0,3,0,2,0,0,7,
0,5,0,1,0,4,0,8,0,
0,0,0,0,3,0,0,0,0,
0,1,0,7,0,9,0,2,0,
5,0,0,4,0,3,0,0,8,
0,0,3,0,0,0,4,0,0,
4,0,6,0,0,0,3,0,1
], Vars
).%%%% AFFICHAGE DU RESULTAT %%%%
printGrid(G) :-
printHSep(3),
printGrid(G,1,1).
printGrid(G,L,10) :-
!,
printHSep(L),
L1 is L + 1,
printGrid(G,L1,1).
printGrid([],_,_) :- !.
printGrid([T|Q],L,C) :-
write(T),
printVSep(C),
C1 is C + 1,
printGrid(Q,L,C1).
printVSep(C) :-
mult3(C), !,
write('|').
printVSep(_) :- write(',').
printHSep(L) :-
mult3(L), !,
nl, write('==================='), nl,
write('|').
printHSep(_) :-
nl, write('|').
mult3(C) :-
T is (C mod 3),
T == 0.Exécution▲
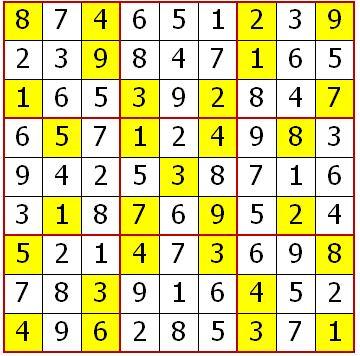
Voici le résultat de l'exécution de ce programme :
?- sudokuExemple(Vars).
===================
|8,7,4|6,5,1|2,3,9|
|2,3,9|8,4,7|1,6,5|
|1,6,5|3,9,2|8,4,7|
===================
|6,5,7|1,2,4|9,8,3|
|9,4,2|5,3,8|7,1,6|
|3,1,8|7,6,9|5,2,4|
===================
|5,2,1|4,7,3|6,9,8|
|7,8,3|9,1,6|4,5,2|
|4,9,6|2,8,5|3,7,1|
===================
|
Vars = [8, 7, 4, 6, 5, 1, 2, 3, 9|...] ;
NoEn appuyant sur la touche « ; » on demande la recherche d'autres solutions. La réponse « No » nous indique qu'il n'existe pas d'autre solution.
Voici donc notre sudoku résolu :
Performances▲
Performances de swi-prolog▲
Lorsque l'on exécute le programme précédent en swi-prolog et son équivalent en Sicstus Prolog, on s'aperçoit que le programme en Sicstus Prolog trouve la solution plus rapidement. Il apparait en effet que swi-prolog n'applique pas systématiquement la consistance d'arc. Ceci se ressent sur les temps d'exécution.
Pour que swi-prolog applique la consistance d'arc (réduction des domaines des variables à chaque ajout de contraintes), il faut utiliser la bibliothèque 'clp/clp_distinct' (consistance d'arc) en conjonction avec la bibliothèque 'clp/bounds'. Les performances se rapprochent alors de Sicstus Prolog.
Ceci nous montre l'importance de la réduction de domaine par propagation de contraintes pour la recherche de solutions.
La section suivante montre le programme modifié pour effectuer la consistance d'arc en swi-prolog.
Programme modifié▲
Notez les différences suivantes par rapport au programme précédent :
- inclusion de la bibliothèque 'clp/clp_distinct' ;
- utilisation du prédicat vars_in/3 ;
- remplacement du prédicat all_different/1 (de clp/bounds) par all_distinct/1 (de clp/clp_distinct).
Par ailleurs, on me rapporte que la bibliothèque 'clp/clp_distinct' n'est disponible qu'à partir de la version 5.5.37 de swi-prolog.
:- use_module(library('clp/bounds')).
:- use_module(library('clp/clp_distinct')).
/*
Permet de résoudre un sudoku
Entrée: +Grid: la grille de sudoku (0 => vide, [1-9] => ajoute une contrainte)
Sortie: -Vars: une solution (permet de savoir s’il existe plusieurs solutions)
*/
sudoku(Grid, Vars) :-
% Definition des variables (grille de sudoku)
Vars =
[
A1,A2,A3,A4,A5,A6,A7,A8,A9,
B1,B2,B3,B4,B5,B6,B7,B8,B9,
C1,C2,C3,C4,C5,C6,C7,C8,C9,
D1,D2,D3,D4,D5,D6,D7,D8,D9,
E1,E2,E3,E4,E5,E6,E7,E8,E9,
F1,F2,F3,F4,F5,F6,F7,F8,F9,
G1,G2,G3,G4,G5,G6,G7,G8,G9,
H1,H2,H3,H4,H5,H6,H7,H8,H9,
I1,I2,I3,I4,I5,I6,I7,I8,I9
],
%%%%% REGLES DU JEU %%%%%
% Les cases prennent des valeurs de 1 a 9
Vars in 1..9,
vars_in(Vars, 1, 9),
% Tous les chiffres d'une ligne sont differents
all_distinct([A1,A2,A3,A4,A5,A6,A7,A8,A9]),
all_distinct([B1,B2,B3,B4,B5,B6,B7,B8,B9]),
all_distinct([C1,C2,C3,C4,C5,C6,C7,C8,C9]),
all_distinct([D1,D2,D3,D4,D5,D6,D7,D8,D9]),
all_distinct([E1,E2,E3,E4,E5,E6,E7,E8,E9]),
all_distinct([F1,F2,F3,F4,F5,F6,F7,F8,F9]),
all_distinct([G1,G2,G3,G4,G5,G6,G7,G8,G9]),
all_distinct([H1,H2,H3,H4,H5,H6,H7,H8,H9]),
all_distinct([I1,I2,I3,I4,I5,I6,I7,I8,I9]),
% Tous les chiffres d'une colonne sont differents
all_distinct([A1,B1,C1,D1,E1,F1,G1,H1,I1]),
all_distinct([A2,B2,C2,D2,E2,F2,G2,H2,I2]),
all_distinct([A3,B3,C3,D3,E3,F3,G3,H3,I3]),
all_distinct([A4,B4,C4,D4,E4,F4,G4,H4,I4]),
all_distinct([A5,B5,C5,D5,E5,F5,G5,H5,I5]),
all_distinct([A6,B6,C6,D6,E6,F6,G6,H6,I6]),
all_distinct([A7,B7,C7,D7,E7,F7,G7,H7,I7]),
all_distinct([A8,B8,C8,D8,E8,F8,G8,H8,I8]),
all_distinct([A9,B9,C9,D9,E9,F9,G9,H9,I9]),
% Tous les chiffres d'un carre sont differents
all_distinct([A1,A2,A3,B1,B2,B3,C1,C2,C3]),
all_distinct([A4,A5,A6,B4,B5,B6,C4,C5,C6]),
all_distinct([A7,A8,A9,B7,B8,B9,C7,C8,C9]),
all_distinct([D1,D2,D3,E1,E2,E3,F1,F2,F3]),
all_distinct([D4,D5,D6,E4,E5,E6,F4,F5,F6]),
all_distinct([D7,D8,D9,E7,E8,E9,F7,F8,F9]),
all_distinct([G1,G2,G3,H1,H2,H3,I1,I2,I3]),
all_distinct([G4,G5,G6,H4,H5,H6,I4,I5,I6]),
all_distinct([G7,G8,G9,H7,H8,H9,I7,I8,I9]),
%%%%% VALEUR DU PLATEAU %%%%%
grid(Grid, Vars),
%%%%% RECHERCHE DE SOLUTIONS %%%%%
label(Vars),
printGrid(Vars).
/*
Permet d'initaliser la grille de sudoku
Pour chaque élément différent de 0,
ajoute la contrainte Var #= Val
*/
grid([],[]) :- !.
grid([0|Q1],[_|Q2]) :-
!,
grid(Q1,Q2).
grid([Val|Q1],[Var|Q2]) :-
!,
vars_in([Var], [Val]),
grid(Q1,Q2).
/*
Un exemple de résolution
*/
sudokuExemple(Vars) :-
sudoku(
[ 8,0,4,0,0,0,2,0,9,
0,0,9,0,0,0,1,0,0,
1,0,0,3,0,2,0,0,7,
0,5,0,1,0,4,0,8,0,
0,0,0,0,3,0,0,0,0,
0,1,0,7,0,9,0,2,0,
5,0,0,4,0,3,0,0,8,
0,0,3,0,0,0,4,0,0,
4,0,6,0,0,0,3,0,1
], Vars
).
/*
Fonction d'affichage du plateau.
*/
%%%% AFFICHAGE DU RESULTAT %%%%
printGrid(G) :-
printHSep(3),
printGrid(G,1,1).
printGrid(G,L,10) :-
!,
printHSep(L),
L1 is L + 1,
printGrid(G,L1,1).
printGrid([],_,_) :- !.
printGrid([T|Q],L,C) :-
write(T),
printVSep(C),
C1 is C + 1,
printGrid(Q,L,C1).
printVSep(C) :-
mult3(C), !,
write('|').
printVSep(_) :- write(',').
printHSep(L) :-
mult3(L), !,
nl, write('==================='), nl,
write('|').
printHSep(_) :-
nl, write('|').
mult3(C) :-
T is (C mod 3),
T == 0.Extension du problème▲
Pour des raisons de simplicité et afin de faciliter la compréhension, nous avons limité notre problème à la résolution de sudoku de 3x3x3.
Cependant, il est tout à fait possible d'étendre le problème à la résolution de sudoku de 4x4x4, 5x5x5 ou de taille quelconque (n x n x n). Dans ce cas, il faut prévoir :
- un prédicat pour la génération des variables du problème ;
- des prédicats pour connaître la liste des lignes, colones et carrés et ainsi pouvoir ajouter les contraintes all_different ;
- le domaine des variables, qui va de 1 à n².
Différences entre swi-prolog et Sicstus Prolog▲
Dans notre article, nous avons mis en avant certaines différences entre swi-prolog et Sicstus Prolog, la première étant le prix puisque swi-prolog est gratuit alors que Sicstus Prolog ne l'est pas.
D'un point de vue technique, on note aussi quelques différences, parmi lesquelles :
- une différence dans le nom des bibliothèques ;
- des différences dans les API, comme la présence du prédicat domain/3 dans Sicstus Prolog ;
- le prédicat labeling/2 de Sictus Prolog propose plus d'options que le label/1 de swi-prolog.
Au niveau performances, le solveur de Sictus parait plus optimisé. Comme nous l'avons vu, le solveur de swi-prolog n'effectue pas de consistance d'arc par défaut, ce qui ralentit la recherche de solution. Sicstus Prolog applique la consistance d'arc sans modification du code, inclut d'autres optimisations et offre plus d'options dans la recherche de solutions.
Dans un contexte industriel, l'acquisition d'une licence Sicstus Prolog peut être envisagée, après étude approfondie. Dans le cadre de petits projets ou de prototypage, swi-prolog peut suffire. (Note: je suis neutre, je n'ai pas d'actions chez Sicstus Prolog !)
Conclusion sur le langage▲
De manière à illustrer le principe de la Programmation Logique avec Contraintes, ainsi que les différentes étapes de sa mise en œuvre (définition des variables, de leur domaine, spécification des contraintes, recherche de solutions), nous avons pris un exemple simple : la résolution d'un sudoku. Cependant, il est tout à fait possible en Prolog de spécifier des contraintes beaucoup plus complexes, faisant notamment intervenir des formules mathématiques (ex: X*X + 5*Y*Y #<= 2*Z*Z + Delta).
Il existe bien entendu de nombreuses bibliothèques permettant de faire de la Programmation par Contraintes dans de nombreux langages. Néanmoins, toutes n'offrent pas la même richesse d'expression que le langage Prolog (que ce soit dans la spécification des contraintes ou dans le mécanisme de « retour arrière » (backtracking) des prédicats Prolog).
Par ailleurs, il est très simple d'interfacer un programme Prolog avec un autre langage (par exemple C++ ou Java), ce qui rend cette solution très attrayante. De plus, contrairement aux idées reçues, l'exécution d'un programme Prolog n'est pas lente du tout, d'autant que la réduction de domaine par consistance d'arc améliore grandement les performances.
Finalement, Prolog nous a permis de développer un programme pour la résolution de sudoku à la fois simple, clair, rapide, propre, très court (environ 200 lignes) et utilisable en conjonction avec d'autres langages.
En outre, cet article aura également été l'occasion de faire un rapide comparatif entre swi-prolog et Sicstus Prolog, notamment dans le domaine de la Programmation Logique avec Contraintes.
En résumé, voici quelques-uns des avantages de la Programmation Logique avec Contraintes dans la résolution de certains problèmes :
- moins de programmation ;
- une programmation simple et claire ;
- moins de risque de bugs (car programmation simple et claire) ;
- exécution rapide (grâce à la propagation des contraintes).
Pour toutes ces raisons, la Programmation Logique avec Contraintes est susceptible d'intéresser les entreprises souhaitant trouver une méthode simple pour résoudre des problèmes parfois complexes et faisant intervenir beaucoup de contraintes. Ces mêmes entreprises pourraient être intéressées par :
- la grande expressivité du langage Prolog ;
- sa facilité d'intégration à un programme écrit dans un autre langage.
Remerciements▲
Je tiens à remercier Trap D pour l'intérêt qu'il a porté à la relecture de cet article et les vérifications effectuées.
Je tiens également à remercier Adjanakis de m'avoir montré certaines solutions existantes dans d'autres langages (C++, Java) en matière de Programmation avec Contraintes, ce qui m'a permis de faire la comparaison avec Prolog. Ces solutions étant assez spécifiques, je n'en citerai qu'une, pour Java : choco, accompagnée d'un exemple de résolution de sudoku avec choco.